
As software developers, we spend a significant portion of our time dealing with logic, be it through conditional statements, loops, functions, and myriad other mathematical and problem-solving constructs to try and make a computer do what we want. I say *“try*” because this process is often based on trial and error, leading to bugs. You could think of bugs in software as flaws in our reasoning when understanding a problem, or a mistake we made when implementing a solution. They are unavoidable, and over time our experience trains us to be better prepared for avoiding some of these issues.
What’s interesting is these kinds of bugs also exist in the way we think and reason about everything in life. Acting irrationally or making emotion-based decisions can eventually make their way into written code and manifest as real-world problems for us and our users. What if we could apply the same rigorous standards to making logical decisions as we do for writing logical, functional software?
This post is the introduction to a series about thinking critically, rationally, ethically, and skeptically about how we write code, looking into the core concepts of logic. We will be taking a look at the basics of logical reasoning, how it applies to decision-making, and in the rest of the series point out a number of common flaws you will encounter and learn to recognize during this process. The introduction outlined here should be considered a primer to logic, and in future posts, we will apply various techniques to example use cases when writing and discussing software.
Note: Since the bulk of the work I do is in JavaScript and React, I will often use such syntax or examples to demonstrate a point.
What is logic anyway?
In computer and electrical systems, logic refers to operations, statements, or controllers that control the flow of data or a signal through the system. Whether physical or virtual, these operations are firmly rooted in determining the truth about something. Every time you compare a value or detect a signal, you are making a determination about whether that comparison is true or not, and making subsequent decisions from there.
Speaking of logic from a mental perspective is not so different. When we need to make a decision, we attempt to reason what is true and what is not and come to a conclusion. Logic is about performing this reasoning correctly. It is my goal to shed light on multiple facets of “correct reasoning” so we can concretely apply it to the way we write software, have discussions, and work together.
When you come to some conclusion in your mind, these thoughts have little consequence on anything in reality until you either need to make a decision based on that conclusion or when trying to convince others to also accept what you have said is true. In order for a statement to be true, that statement must demonstrate it is “valid” and “sound”. We will dive into what these mean soon, but first let’s take an aside into some ground rules about statements we make.
Laws of Logic
There are three traditional laws of logic: widely-accepted axioms that form the basis for declaring truth. Let’s examine them.
Law of identity
This is a little esoteric, but in a nutshell says that given a value, it is identical to itself. Developers who utilize functional programming should be familiar with concepts of identity and its application, but finding a real-world purpose for knowing that “this dog is a dog” or true === true seems silly. I will point out how identity comes into play in a future post about equivocation, and for now just take this law into consideration.
Law of non-contradiction
This law states that you cannot make two statements that contradict each other and have both of them be true at the same time, at least in the same sense. In JavaScript, we can demonstrate this with:
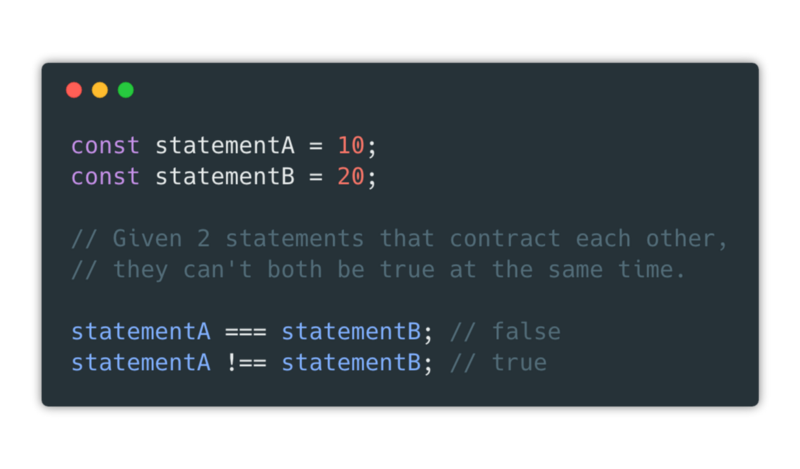
This applies to practically anything you declare. For example:
Person A: “Angular has more users than React!”
Person B: “No, React has more users than Angular!”
These statements are *mutually exclusive**:* they contract each other, and therefore both of them cannot both be true at the same time. This may seem like common sense, but understanding this is important in a conversation where such contradictions may not have been so pointedly declared.
Law of excluded middle
This one is similar in form to the law of non-contradiction, and says that given a statement, it is either true, or its opposite form is true; there is no third option (the excluded middle option).
Using another code sample, let’s take a look:
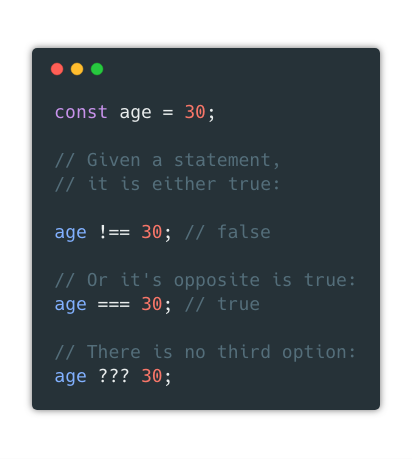
Let’s again look at the conversation about which package has more users:
Person A: “Angular has more users than React!”
Person B: “No, React has more users than Angular!”
Since both of these statements are mutually exclusive, we know from the law of non-contradiction, that they cannot both be true at the same time. But if we look carefully at the statements, we can also see that each is the opposite proposition as the other. This means that we can know that one of these statements is true, and the other is false.
You may be thinking, “These laws just sound like common sense to me!” If so, that’s great! It is still important to realize their significance in decision-making, and you can see their influence in finding flaws in our reasoning in future posts.
Validity
When you make an assertion about something, your argument is said to be valid if the truth of your premises can guarantee that your conclusion is also true. We are not really evaluating the claim itself here, but rather the form of the claim, as an invalid claim cannot be true.
Kat prefers either Redux or MobX.
Kat does not prefer MobX.
Therefore, Kat prefers Redux.
This argument is logically valid because the premises follow the conclusion. Given our initial statement about whether Kat prefers Redux or MobX, if our second statement is true, then the conclusion is guaranteed to be true. If our second statement is false, our conclusion is guaranteed to be false. A valid argument does not guarantee truth, though:
All arrays have a length property.
This object has a length property.
Therefore, this object is an array.
This argument is still technically valid; it is possible for an object to be an array, but not all objects are arrays, even if they have a length property. If the object didn’t have a length property, it would be impossible for it to be an array! Again, determining the validity of an argument is about the form of the argument and not its actual content. To continue our quest for truth, we evaluate the content for soundness.
Soundness
An argument is considered sound when its premises are actually true, and also valid. This part does take the content of the statement into consideration.
GitHub is the most popular version control platform.
GitHub says JavaScript is the most popular language on its platform.
Therefore, JavaScript is the best language.
Premise 1 could probably be demonstrated to be true, and Premise 2 is true according to GitHub. But the conclusion cannot logically follow and be demonstrated to be true based on this. This argument is unsound. Whenever we uncover a bug in our reasoning from the structure of our statements, we call this a logical fallacy. Identifying and resolving logical fallacies will be done extensively in this series.
Why should I care about logic when making decisions?
Using correct reasoning keeps our feet firmly planted in reality, and closes the gaps in our arguments that may be irrational. But why should that matter? In order to successfully prove anything you want to assert or convince others to follow a path or make a decision you prefer, you are at risk of losing this battle if your arguments are invalid or unsound. Everyone likes to win, and when you speak correct statements which bring evidence and truth, you have a much greater chance of succeeding in your case as opposed to making irrational arguments. When others are trying to convince you of something, being able to evaluate what they are saying for correctness is also valuable, as it lessens your risk of going down a path of mistakes and wasted time if you can avoid it. Wouldn’t it be nice to guard against this if possible?
Skepticism
Skepticism is the position we take to guard ourselves against accepting claims prematurely; in a word: doubt. The human psyche, while quite advanced, is by no means perfect. We are susceptible to sympathy, deceit, and a whole host of emotional or fallible mental attacks, whether with purposeful intent or by well-meaning individuals. Believing something for which there is no evidence can cause us to make incorrect decisions, make invalid assumptions, or cause harm to other people because of these actions. In order to reduce this risk of harm as much as possible, we take the default position of skepticism: we withhold the right to accept someone’s claim until they have sufficiently demonstrated that claim with evidence.
If someone is accused of a crime, a claim of guilt is made against them. The default position is, therefore, one of innocence until it can be demonstrated with sufficient evidence that there is guilt. Those making a claim are tasked with providing this evidence, and subsequently, carry the burden of proof. The burden of proof lies with the person making the claim, and from a skeptical perspective, that which is declared without evidence may be dismissed without evidence. In a nutshell, if someone makes an assertion without any evidence or solid reasoning to back it up, you are not obligated to accept it as true and may withhold any acceptance or denial of that assertion.
Application in Software
Now that we have a few glossary terms under our belt, how does any of this apply to writing or discussing software? Having the ability to recognize logical pitfalls and irrational reasoning are the foundational aspects of such things as:
- Evaluating tradeoffs in technology decisions
- Debating software practices, patterns, time estimates, minimum viable products, and experimentally testing assertions
- Working cohesively as a team and community by engaging in open dialogue responsibly, ethically, and rationally
In the next several posts, I will outline a number of the logical traps we can fall into in these situations, and hopefully, give you the awareness to recognize and combat them when they arise.
Until next time!